函数式的动态规划

动态规划是一类很常用的算法，在C/C++/Java中一般使用于数组进行记忆化。而函数式编程语言一般无法方便地操作数组这些依赖副作用的数据结构，函数式的记忆化便要另寻他法。

本文就是一个简单的笔记，用一些代码片段展示我所知的函数式动态规划的技巧。

Course-of-Values Recursion

Course-of-Values Recursion是我认为最直观的一种技巧，就是将遍历过的结果当作返回值的一部分保留下来，在递归的时候可以取得运算过的值。

对于递归函数f，定义一个辅助的函数bar

\begin{align} \overline{f}(n) = [f(n), f(n-1),...,f(0)] \end{align}

则原递归函数f可以用bar表示出来：

f(n) = head(\overline{f}(n))

斐波那契数列：


xxxxxxxxxx
fibBar :: Int -> [Int]
fibBar 0 = [0]
fibBar 1 = 1:fibBar 0
fibBar n = let course = fibBar (n-1) in -- [fib(n-1)..fib(0)]
           let p  = course !! 0 in -- fib(n-1)
           let pp = course !! 1 in -- fib(n-2)
           p + pp : course
           
-- >>> fibBar 10
-- [55,34,21,13,8,5,3,2,1,1,0]
--

Binary Partitions：

数的二次幂拆分方法有多少种，其状态转移方程为：

\begin{align} a_0 & = 1 \\ a_{2n} & = a_{2n - 1} + a_{n} \\ a_{n} & = a_{n-1} \end{align}

则：


xxxxxxxxxx
bpBar n
  | n == 0 = [1]
  | even n = let course = bpBar (n-1) in
             let pred = course !! 0 in                 -- bp (n-1)
             let half = course !! (n-1 - n `div` 2) in -- bp (n/2)
             pred + half : course
  | otherwise = let course = bpBar (n-1) in head course : course
  
-- >>> bpBar 20
-- [60,46,46,36,36,26,26,20,20,14,14,10,10,6,6,4,4,2,2,1,1]
--

但遗憾的是，其复杂度并不是O(n)，因为每次都会索引链表，这很糟糕。

0-1背包问题：

其状态转移方程为：

\begin{align} Knapsack(0, y) & = 0 \\ Knapsack(i, y) & = Knapsack(i-1, y) & \text{if}\ w_i \ge y \\ Knapsack(i, y) & = max(Knapsack(i-1, y), v_j + Knapsack(i-1, y-w_i)) & \text{otherwise} \end{align}

这里也需要将这个n*W状态空间塞到course里：

\begin{align} \overline{Knapsack}(i, y) = &[Knapsack(i, y), Knapsack(i, y-1),...,Knapsack(i, 0),\\ &Knapsack(i-1, capacity),...,Knapscak(0, 0)] \end{align}

则：


xxxxxxxxxx
type Weight = Int
type Value = Double
type Items = [(Weight, Value)]
knapsack :: Items -> Weight -> Value
knapsack items capacity = head $ bar items capacity where
    bar :: Items -> Weight -> [Value]
    bar []             0 = [0]
    bar (_:items)      0 = 0 : bar items capacity
    bar []             y = 0 : bar []    (y-1)
    bar ((w, v):items) y
        | w <= y = let course = bar ((w, v):items) (y-1) in
                   let v1     = course !! capacity in        -- knapsack(i-1, y)
                   let v2     = course !! (capacity + w) in  -- knapsack(i-1, y-wi)
                   let new    = max v1 (v2 + v) in
                   new : course
        | otherwise = let course = bar ((w, v):items) (y-1) in 
                      course !! capacity : course
                      
                      
-- >>> knapsack [(2, 6.0), (2, 3.0), (6, 5.0), (5, 4.0), (4, 6.0)] 10
-- 15.0
--

CoV除了经常要索引链表意外还有其它限制，并非所有的递归函数都能转化为这种形式，比如阿克曼函数（Ackermann's function）。

Streaming

这是专属于Haskell的优雅的方法。

斐波那契数列就是一个经典的例子：


xxxxxxxxxx
fibs :: [Integer]
fibs = 1:1:zipWith (+) fibs (tail fibs)
-- >>> take 10 fibs
-- [1,1,2,3,5,8,13,21,34,55]

需要把fibs看作一个流，fibs前两个元素为1且剩余部分由其自身(fibs)与自身去首(tail fibs)合成(zipWith (+))。取“下一个”的时候才会计算，并且不会重复计算，这就是Haskell惰性求值的威力。

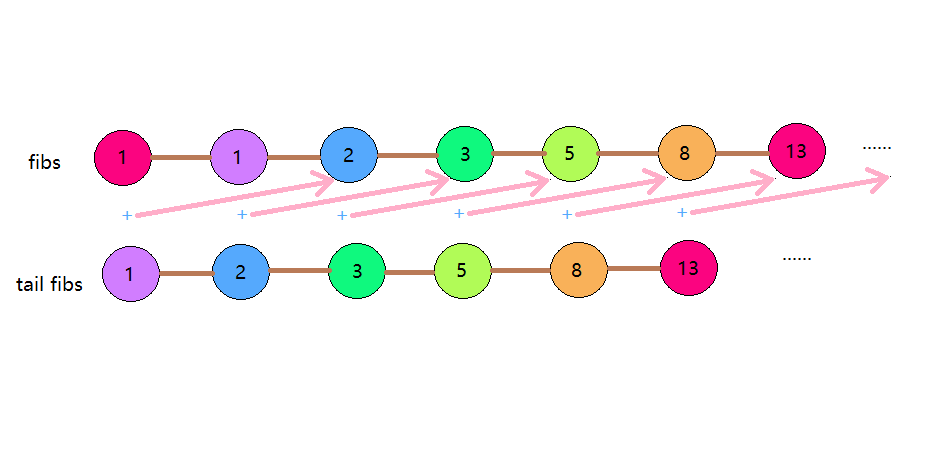
fibs stream

类似的，阶乘流由[1..]和其自身合成：


xxxxxxxxxx
facts :: [Integer]
facts = 1 : zipWith (*) [1..] facts
-- >>> take 10 facts
-- [1,1,2,6,24,120,720,5040,40320,362880]
--

流还可以表达更复杂的问题，比如刚刚的Binary Partitions：


xxxxxxxxxx
bps :: [Integer]
bps = 1:zipWith3 reduce 
          [1..] 
          bps 
          (tail $ dup bps) -- bp (n/2) 组成的流
  where
  dup xs = xs >>= \x -> [x, x] -- 每个元素个数*2
  reduce n a b
    | even n    = a + b
    | otherwise = a
-- >>> take 21 bps
-- [1,1,2,2,4,4,6,6,10,10,14,14,20,20,26,26,36,36,46,46,60]
--

可以发现顺序是和CoV的反过来的。同时，这里还没有了索引的开销，很O(n)，很棒。

流的形式很优美，当然也很少的情况能将流写的很优美，毕竟算法本身就是丑陋的，比如刚刚0-1背包问题换成什么写法都只能写得这样丑陋（但这已经是很简单的算法了）。

Dynamorphism

dynamorphism是recursion schemes的一种，是anamorphism和histomorphism的组合，由anamorphism构造递归树，由histomorphism完成记忆化和规约。

过程上可以看作是CoV的抽象，自动完成记忆化和递归，并且推广了course的结构（但一般还是用List）。


xxxxxxxxxx
-- dynamorphism
dyna :: Functor f => (a -> f a) -> (f (Cofree f c) -> c)  -> a -> c
dyna phi psi a = let x :< _ =  h a in x where
  h = uncurry (:<) . (\a -> (psi a, a)) . fmap h . phi
-- dyna phi psi = histo psi . ana phi

Binary Partitions：


xxxxxxxxxx
bpDyna :: Integer -> Integer
bpDyna = dyna phi psi where
  phi 0 = Nil
  phi n = Cons n (n - 2)
  psi Nil             = 0
  psi (Cons n course) 
    | even n = let pred = fromJust $ lookupCourse course 0 in
               let half = fromJust $ lookupCourse course (n-1 - n `div` 2) in
               pred + half
    | otherwise = fromJust $ lookupCourse course 0
    
lookupCourse :: (Num n, Eq n) => Cofree (ListF e) a -> n -> Maybe a
lookupCourse (x :< _)    0 = Just x
lookupCourse (_ :< hole) n =
  case hole of
    Nil         -> Nothing
    Cons _ next -> lookupCourse next (n - 1)
    
    
-- >>> map bpDyna [0..20]
-- [1,1,2,2,4,4,6,6,10,10,14,14,20,20,26,26,36,36,46,46,60]
--

最长公共子序列：

也是一道经典的dp题，我也不再赘述内容，其状态转移方程为：

\begin{align} lcs([], ys) & = [] \\ lcs(xs, []) & = [] \\ lcs(x:xs, y:ys) & = x:lcs(xs, ys) & \text{if } x=y \\ lcs(x:xs, y:ys) & = lcs(x:xs, ys) & \text{if } \#lcs(x:xs, ys) \gt \#lcs(xs, y:ys) \\ lcs(x:xs, y:ys) & = lcs(xs, y:ys) & \text{otherwise} \end{align}


xxxxxxxxxx
lcsDyna :: Eq a => [a] -> [a] -> [a]
lcsDyna as bs = dyna phi psi (as, bs) where
  aslen = length as
  phi     ([], [])   = Nil
  phi all@([], y:ys) = Cons all (as, ys)
  phi all@(x:xs, ys) = Cons all (xs, ys)
  psi Nil = []
  psi (Cons ([], _) _) = []
  psi (Cons (_, []) _) = []
  psi (Cons (x:_, y:_) course)
    | x == y = x : zs
    | length xs > length ys = xs
    | otherwise = ys
    where
      xs = fromJust $ lookupCourse course 0
      ys = fromJust $ lookupCourse course aslen
      zs = fromJust (lookupCourse course (aslen + 1))

0-1背包问题


xxxxxxxxxx
knapsackDyna :: Items -> Weight -> Value
knapsackDyna goods w = dyna phi psi (goods, w) where
  phi ([], 0)       = Nil
  phi (wv:goods, 0) = Cons (wv:goods, 0) (goods, w)
  phi (goods, w)    = Cons (goods, w) (goods, w - 1)
  psi Nil              = 0
  psi (Cons ([], _) _) = 0
  psi (Cons ((w', v'):goods', rest) course) 
    | w' > rest  = fromJust $ lookupCourse course w  -- course[i-1][w]
    | otherwise =
      let v1 = fromJust $ lookupCourse course w      
          v2 = fromJust $ lookupCourse course (w' + w) -- course[i-1][w - w']
      in  max v1 (v2 + v')
      
-- >>> knapsackDyna [(2, 6.0), (2, 3.0), (6, 5.0), (5, 4.0), (4, 6.0)] 10
-- 15.0
--

另外，这里的recursion schemes的库是直接在hackage里找的。懒得自己写了。dynamorphisim的介绍，我可能会令写一篇文章吧（咕咕咕）。其实我觉得这也没减少什么复杂度。。。

Memocombinators

（更新于2020/5/17，就不新开水文了）

这是个十分简洁美观，几乎在各方面吊打上面几种写法。但这方法本身又挺tricky的，和haskell处理partial application的方式有关。

记忆化最直接的方式，便是维护一个表，用于缓存已计算的结果。比如：


xxxxxxxxxx
-- 接受一个函数，返回其记忆化的版本
memoize :: (Int -> a) -> (Int -> a)
memoize f n = map f [0..] !! n

缓存的内容便是map f [0..]。我们希望该函数有记忆化的效果，那么斐波那契数列就可以写成这样：


xxxxxxxxxx
fibMemo :: Int -> Integer
fibMemo = memoize fib where
    fib 0 = 0
    fib 1 = 1
    fib n = fibMemo (n - 1) + fibMemo (n - 2) 
    -- 这不能调用fib本身，因为fib本身并没有通过memoize进行记忆化

但很遗憾，根本没有起到记忆化的效果。究其原因，当每次调用memoize的时候，都会重新计算一次map f [0..]。

pity

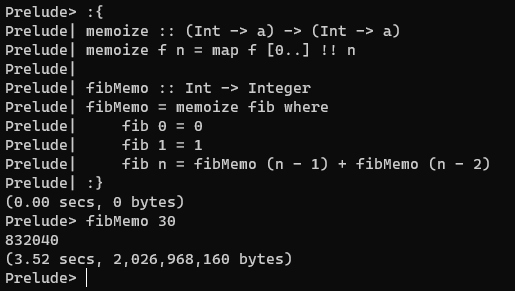
那正确的写法究竟是怎样呢——partial application：


xxxxxxxxxx
memoize :: (Int -> a) -> (Int -> a)
memoize f = (map f [0..] !!) 
-- eq to `(!!) (map f [0..])` 
-- but not `\n -> map f [0..] !! n`

Magically, it works!

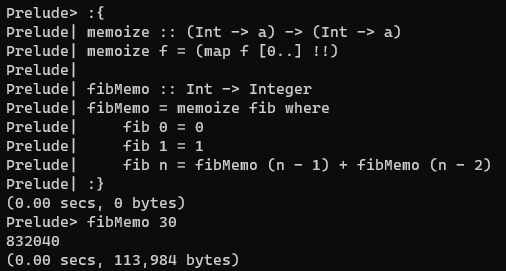
magically

这是因为，在hs中，partial application是不会进行reduce的，仅仅绑定了参数。在memoize中参数(map f [0..])与函数(!!)绑定，于是整个过程map f [0..]只会产生一次（一个thunk）。于是利用(map f [0..])缓存下f计算过的值，从而达到memoization的效果。

但是\n -> map f [0..] !! n这样是不行的，每次调用都会重新计算一遍map f [0..]。

在hs中，只有在“完整调用”的时候会进行reduce(call)，而在“部分调用”（partial application）的时候做的只是参数的绑定（bind）。这就导致了η变换在hs中并不完全等价，而且会导致记忆化的“丢失”。（这里应该还可以引入CAF(Constant applicative form)，此处不展开了）

同理，如果将fibMemo写为：


xxxxxxxxxx
fibMemo :: Int -> Integer
fibMemo n = memoize fib n where
    -- ...

也将没有了记忆化的效果。所以这个方法是一个很tricky的方法，利用了hs不那么一致的“feature”，才有这样的效果。

另外，单链表索引太慢，我们也可以使用其它的数据结构来进行缓存——二叉搜索树、(hs中只读的)数组、哈希表等等（上面的CoV也可以）。总之memoize的一个通用的形式为：


xxxxxxxxxx
memoize :: (k -> v) -> (k -> v)
memoize f = index (fmap table f)

可以抽象为一个typeclass：


xxxxxxxxxx
class Memoizable k where
    memoize :: (k -> v) -> (k -> v)

对于复杂类型的记忆化，可以基于Map的以下几条性质：


xxxxxxxxxx
Map () v           ~ v
Map (Either a b) v ~ (Map a v, Map b v)
Map (a, b) v       ~ Map a (Map b v)

可以导出Memoizable k的性质：


xxxxxxxxxx
Memoizable ()
(Memoizable a, Memoizable b) => Memoizable (Either a b)
(Memoizable a, Memoizable b) => Memoizable (a, b)
-- 分别实现

我们可以得到一些很有用的函数：


xxxxxxxxxx
-- 记忆化两个参数。
memoize2 :: (Memoizable a, Memoizable b) => (a -> b -> r) -> (a -> b -> r)
memoize2 = curry . memoize . uncurry
-- 记忆化第二个参数
memoizeSecond :: Memoizable b => (a -> b -> r) -> (a -> b -> r)
memoizeSecond = flip . memoize . flip

现在可以来做个背包问题：


xxxxxxxxxx
knapsackMemo :: Weight -> Index -> Value
knapsackMemo = memoize2 knapsack where
    knapsack y 0 = 0
    knapsack y i
        | wi >= y   = knapsackMemo y (i - 1)
        | otherwise = max (knapsack y (i - 1)) (vi + knapsack (y - wi) (i - 1))
        where
            ~(wi, vi) = items !! i

十分简洁，就是直接写上状态转移方程。

但总的来说，这种美观却tricky的方法是没有保障的，hs也并没有承诺它会对partial application进行bind的处理，更是一种接近于UB的存在。写起来也要十分的小心，当代码复杂起来，可能一个不小心写法上不对，就丢掉了“记忆化”。慎用。

Addition：


xxxxxxxxxx
-- 记忆化函数更好的写法
fib f 0 = 0
fib f 1 = 1
fib f n = f (n - 1) + f (n - 2)
fibMemo = fix (memoize . fib)
-- -> memoize (fib fibMemo)

总结

没啥想总结的23333。总之，我觉得除了streaming以外，都很丑陋。recursion schemes也是，还是最多用到hylomorphism就算了，同时我认为应用将recursion schemes在“不是处理数据”的递归上，也不是正确的用途，因为这并不直观。

新更新的Memocombinators在hackage中有同名的库：

https://hackage.haskell.org/package/data-memocombinators

前两天hs群里提到了该方法：

https://wiki.haskell.org/Memoization

看到该方法的时候，我便感到十分地羞愧（因为本文之前提到的方法过于繁杂，甚至可以说没啥用），十分的兴奋，却也同样十分地不解——究竟是怎么利用thunk进行记忆化的？后来得到店里的指导（我太菜了，不好意思@他们），才了解到区别，对此十分感谢。