啥是Monad
Attention: 本文不是讲Monad,而是Head First Category For Myself。始于群,止于Monad。
(也写给未来的自己,回头看看这篇傻傻的文章,然后感到一些羞耻。。。)
文章结构:
群(Group)
范畴(Category)
一些概念的反哺
- 幺半群(Monoid)
- 群(Group)
- 偏序关系(Partial Order Relation)
- 集合(Set)
0和1,+和×,极限与与余极限
- 0和1
- +和×
- 极限和余极限
米田引理(Yoneda Lemma)
- 函子(Functor)与自然变换(Natural transformation)
- 米田引理及其推论
计算的三位一体论(Computational Trinitarianism)
所以啥是Monad
总结
群(Group)

为啥从群开始?因为其实范畴本身也是一种代数结构,所以为了找回理解群时那种感觉(去接受范畴这种抽象),我们先来温习下群的定义,顺便讲讲一些“注意事项”。
定义1.1
群G包含一些数学对象:
- 一个单位元:
- 一个二元运算:
- 一个逆运算:
- 一些元素:
满足(有规则):
- 单位元:
- 结合律:
- 逆元:
我们用一个元组来表示一个群:
也可以借用集合的符号,将群表示为一个 元素的集合 与 二元运算 的二元组
必须得澄清一下:
- 在这个定义中,我是将群从集合论中剥离了开来(甚至丢掉了逻辑结构),而将其看作一个独立的形式系统来看待,目的是为了先把”集合“这种概念忘掉,让脑子干干净净地接受一些不同的思维与视角。
- 虽然说了借用集合的符号,但并不意味着群依赖于集合论,而是作为类似”语法糖“的东西,便于后续的表达与理解。
- 不过将群从集合中剥离出来之后,一些定理就必须先在原先的系统中附加一些结构才能表达,比如说子群、商群、同态等等。
- 值得注意的还有这里的相等,这里的相等是系统定义中符号意义上的相等,作为一种运算规则而存在(或者是基本的二元关系),而不是在系统内定义的等价关系意义上的相等(比如在集合论内用关系定义的相等),层次不一样。后者可以作为系统中的对象来研究,而前者是一种基本的语素。
- 除了相等,还有其它的东西要分清层次,比如有“1”个单位元,不代表这群论就依赖于自然数了,这同样是元层次上的“1”。这和相等一个道理。
在下面的各种定义也基本是这个理儿。
稍等片刻,那么,在F5脑子*n后,准备好接受新东西了吗?
范畴(Category)
先来谈谈“动机”。
- 集合论(最先是朴素的集合论)关注的是研究对象的内在属性与组成,于是把对象的性质抽象了出来,得到了集合的概念。
- 群论关注的是研究对象的某些运算性质,于是把元素以及其上的二元运算抽象了出来,得到了群的概念。(当然,最初是用来解决一元五次方程根式解的问题的)
范畴也有这样的动机(这可能不是数学家们最初的想法)
- 范畴论关注的是研究对象之间的相互关系,于是把这些相互关系抽象为了对象间态射(Morphism),就得到了范畴。
其实集合与范畴可以分别对应着两种不同的哲学思想。集合论就是典型的还原论的思想,侧重的是研究对象的内在属性与组成,并作归纳。与之相对应的,范畴论则是一种演生论(holism)的思想,侧重的是对象之间的关系,并作推演,从整体的结构着手,而非具体对象本身。
将人作为研究对象为例(不恰当的例子),集合论侧重于研究其本身的特质,而范畴论则研究其发生的社会关系——人的本质是一切社会关系的总和。
在有了一些直观的认知之后,可以引入范畴的定义了(也稍微借一借集合中的符号)。
定义2.1
范畴包含一些数学对象:
一些对象(objects): ,
记为
一些对象上的态射(morphisms): ,
记为,其中对象A到对象B上的所有态射记为
特别的,每个对象上的单位态射:
一个态射上的复合运算(compose):
其中态射满足:
- 结合律:
- 单位元:
值得注意的是,范畴论并不关注对象的“内部”特征,对象可以是任意东西;那么同样的,态射也可以是任意东西,任意对象和对象的关系,而不应理解为对象A到对象B的函数、变换等具有显著的集合论意义的东西。
就像你学集合的时候立刻能想到的“袋子模型”,你现在也可以将范畴联想为一些带有点和箭头的“有向图”:
事实上,范畴论的证明和定义通常会用一些交换图来展示:
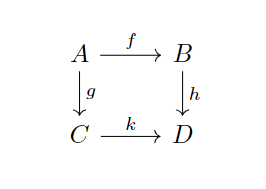
比如上图就表示
范畴的定义很精简,其代数结构比群还要简单,而不像公理化集合论那么复杂,既要用公理给出集合的限制性的构造,又要用公理防止悖论的出现。相对于集合论丰富的公理系统,上手即可表达各种各样的对象和命题,范畴论则需要附加上一些其它的结构,才能表述各种丰富的命题,这点和各种代数系统是一致的。
那么范畴作为一种十分广泛的抽象,我们尝试着用它来描述一些常见的数学对象。
一些概念的反哺
幺半群(Monoid)
我们发现,范畴的态射与态射的复合 和 幺半群的元素与二元运算 要求的law是一致的——都是单位元和结合律。其中只有单位元律有所区别,态射的单位元每个对象都有一个,但这十分好处理,我们只看其中一个对象上的态射就好。
这便非常自然地引导出了我们的第一个定义。
定义3.1.1:只有一个对象的范畴称为幺半群。
再唠叨一遍,这个"1"个对象也是元层面上的"1",是范畴定义之初给的,以后说的“存在唯一一个态射”的“存在唯一”同样也是,既不依赖于"1"本身,也不依赖于“存在”。
那么,一个半群的元素便是范畴的态射,半群的二元运算便是态射的复合。于是我们便成功地把幺半群放到范畴的框架之中了,非常自然,非常trivial。(不要想那个对象里究竟有什么)
群(Group)
经典的代数理论中,群在幺半群上仅仅是多附加一个“逆”的结构,在态射的语境中也有对应的概念,可逆态射,或是isomorphism(同构态射?)。isomorphism可以看作一个”双箭头“,或者说箭头两侧的对象可交换的箭头,不过这里就不给出isomorphism的定义了。
那么也可以很自然的在范畴的框架中给出群的定义:
定义3.2.1:只有一个对象且所有态射是isomorphism的范畴称为群。
但习惯上,从范畴论出发来定义一个群,则先描述一种称之为群胚(Groupoid)的特殊的范畴。
定义3.2.2:所有态射都是isomorphism的范畴称为群胚
然后群就是只有一个对象的群胚,特别形象。(题外话,不加任何限制的范畴是不是叫做幺半群胚,Monoidoid?不过并没有这样的说法。)
群胚这种范畴用途很广,最常见的便是用于描述对象的等价性(但可能有多种使得对象相等的方式),比如HoTT中类型和univalence就组成了一个群胚。
再进一步,如果我们给对象再加点要求——对象是“态射的不动点”,那么“态射组合可交换”则又是自然成立的了,然后我们就得到了个阿贝尔群(Abel Group)。不过这个要求相对就不那么”廉价“了。(这里就请容许我作这样不严谨的表述)
偏序关系(Partial Order Relation)
偏序关系满足:
- 自反性:
- 反传递性:若, ,则
- 传递性:若, ,则
这也可以很自然的放入到范畴的框架里去——作为对象间的态射,其自反性和传递性恰好满足了 态射的单位元律和结合律;而偏序关系中的元素则作为范畴中的对象。
此时我们的态射是一个二元关系,而在群中可以作为元素,在集合中可以是函数或叫映射。范畴并没有对对象和其态射做任何规定,它们可以是任何东西,只要满足范畴的性质,就可以套入范畴的框架下讨论。同时也应该可以看到范畴涵盖的东西是极其广泛的,甚至可以断言——没有比对象间关系更基础的东西,一切都东西都可以用范畴来表达。
集合(Set)
让我们回到集合的世界,尝试用范畴来描述集合,但可能这在范畴论中属于最无趣的工作了。
定义3.4.1:只有单位态射的小范畴是集合
有几点需要解释
- 范畴中的对象作为集合的元素,范畴中的态射表示元素的相等
- 只有单位态射很好理解,集合要求元素有互异性,也就是每个元素只和自己相等
- 小范畴,指的是, 都是集合的范畴。这里还需要解决一下循环定义的问题,大概的解决办法还得引入一个Size的结构,总之复杂度相当于用范畴的语言重新造了个ZFC,这里就再展开了。不过在HoTT中——一个,集合则以另外一种更有趣更简洁的方式去定义,有机会再讲讲。
这么无趣的范畴,一般不去讨论,但这里顺便引入了一个小范畴的概念,方便后续讨论:
定义3.4.2:对于范畴,若,是集合,则范畴是小范畴;如果所有是集合,则范畴是局部小范畴
虽说集合本身作为一个范畴很无趣,但我们至少有了集合的概念。集合与集合之间的关系(函数)还是很有趣的,我们可以定义一些常见的范畴:
- 定义3.4.3:所有集合的范畴记为,态射为集合间的函数
- 定义3.4.4:所有向量空间的范畴记为,态射为线性变换
- 定义3.4.5:所有群的范畴记为,态射为群之间的同态
- 定义3.4.6:所有拓扑空间的范畴记为,态射为连续函数
……
其中, , 等等范畴可以看作是畴附上结构一些得到。
0和1,+和×,极限与与余极限
上面一些定义还体现不了范畴论的思想,可能大家看完之后还会流露出稍微鄙夷的感情——”就这?就这?“,”把已有的概念复读一遍,有什么好玩的“。。。为了打消大家对范畴论的疑虑,接下来我打算从0和1开始,尝试用范畴论的思想思考问题,用范畴论来解决问题。(然而事实是我看着几个箭头用”格物致知“的方式生编硬造出来的诡吊牵强又拙略的解释方式。。。)
0和1
不知道大家还是否记得学习数数的过程。以”1“为例,我们总是被教导:”‘1’个苹果是‘1’,‘1’根香蕉是‘1’,……”。

如果我们的学习过程是集合的,那么以各种“1”的代表教导“1”的过程,大概就是在脑海里建立了一个 “所有‘1’的代表” 的集合:
然后数数,便对应着判断是否属于1这个集合:
然而我们学习的过程真是如此么?不知道大家注意到了没有,这仅仅对应着学习中归纳的过程,我们也不会真正将所有的“1”记在脑子里,这就缺少了我们常说的“举一反三”,而这才是我们真正习得知识的途径。如果仅仅学习只是归纳的话,我们在以后的学习中,我们或许就不能那么轻松地理解各种抽象的“1”了。
不知道大家学习新概念的时候,有没有这样的体会:我们将各种各样的实例塞到脑子里,脑袋懵懵,然后过几天好像就突然开窍了一般,“理解”了这个知识。这是“集合化的学习过程”所无法解释的。我们学习的过程不是集合化的,但可能是范畴化的。我们之所以能在不同的语境下,轻松地找到对应的“1”,是我们潜意识里注意了“1”和其它东西的关系了:
- “1”个苹果,是因为我们(只能)看到了它;而两个苹果,我们可以看着“这一个”,也可以看着“那一个”,所以这不是“1”;没有苹果,那我们就啥也看不到,那也不是“1”。这里以“看见”为“我”和“苹果”的关系,展示了”1“的本质(唯一的关系)。
- 实数里的”1“,只有1和其它实数(除了0)相乘不变;而2不行,0也不行。这里以”相乘不变“为其它实数x和1的关系,展示了”1“的本质(要是有两个1之间也是同构的)。
- 全集作为”1“,所有集合都包含于全集;而空集做不到(除非全集是自身)。这里以”包含“作为集合与全集之间的关系,同样也展示了“1”的实质(1还得是普适的)。这就和数数的“1”原本用于数数的意义差的远了,但我们还是能很自然地将它当成了1.
看出来了吗,用范畴论的语言来说,就是这样一个图(虚线表示唯一):
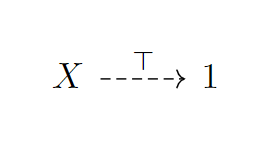
解释一下就是:
定义4.1.1:在一个范畴中,所有对象对于作为的对象存在唯一的态射。称为终止对象(terminal object)。
当然,也不是所有的范畴中都有这么些“1”。另外稍微补充一下后两个例子,实数相等的方式是唯一的,集合包含的方式也是唯一的,也符合范畴所描述的关系。
看,我们其实从来不需要关心”1“究竟是什么,只要某个东西和其它东西的关系像”1“,就可以把它当作(在当前语境中的)“1”,这才是我们从各种不同的“1”的归纳中习得的东西,认识“关系”就是”举一反三“能力的来源。那这时有人可能会疑惑,既然认识到“关系”才是学习某个知识的一个“终点”,那为何不直接学习关系,还要灌输大量的实例呢?我觉得大概有两个原因:
- “关系”不是那么好找的,难以总结,难以教授,还是得通过归纳和积累,才能将这种内在的“关系”内化成自身的知识。说白了就是还是得靠脑子,而实例本来就很抽象的知识脑子不行就很难学了。
- 我们的知识体系已经在“去范畴化”的路上越走越远,重新用范畴的语言去描述,或许还需要些时日。或者说范畴论本身还不够完善和成熟。
另外在范畴论的语言中,对象还有其它用处。就是用态射表示“内部的元素”,在范畴论中称之为”广义元素“(generlized element),那么我们常写的便改写为。虽然在范畴论中不关心对象的内部,没有专门的描述对象”内部“的语法(比如集合中的),但其实我们仍然可以通过态射表示对象“内部”的信息。这其实也是很”自然“的,比如。。。粒子加速器?
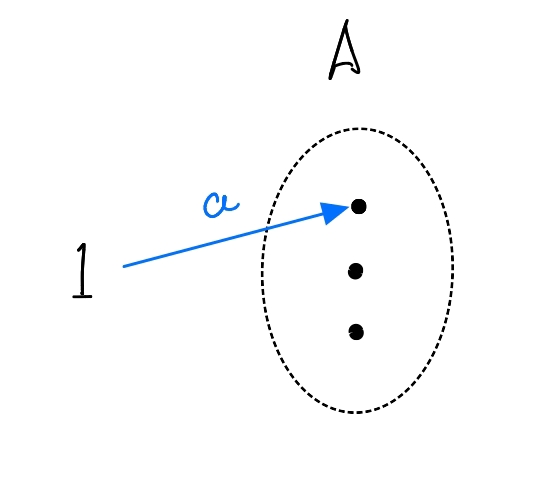
“1”说完了,“0”也是类似,但我不想解释了,大家可以体会吗:
定义4.1.2:在一个范畴中,作为的对象到所有对象存在唯一的态射。称为初始对象(initial object)。
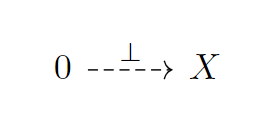
精彩的是,0和1的其实就是把箭头反转了过来了而已,其实这就是体现了两者的对偶关系。而事实上我们学的众多的“0”和“1”之间都有这样的对偶关系,0和1,true和false,空集和全集等等。
+和×
讲完了0和1,我们终于可以来讲1+1了。其实相对于1来说,1+1的区别就是多了一个选择,或者说+天然表示某种可选的性质:
- 🍎🍎,我们可以拿左边的一个苹果,也可以拿右边的一个苹果,这是选择。
- 分配律,对于来说,这也代表一种选择。
- 事件/命题/集合的或也可以看作一种选择,表示可以选择也可以选择。
那么用范畴的语言来说,就可以表达为一个图
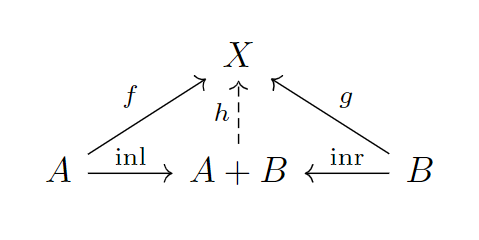
定义4.2.1: 在一个范畴中,对于对象和对象,如果与的和存在,则由两个态射唯一确定。满足对于所有对象和态射,到存在唯一的态射,使得以及。
这时定义相比于交换图来说就显得十分的冗长了。总之是由两个态射所定义的。
稍微解释一下定义中表述“选择”的地方。唯一的态射,我们可以写成,然后表示如果在中选择则使用态射,表示如果选择则使用态射。

而×代表某种“我全都要”的性质:
- 5行3列的🍎,表示我同时拥有了5行的🍎和3列的🍎。(好像是废话。。。)
- 一个自然数可以分解为,“同时拥有”了。
- 事件,表示同时发生。
那么用范畴的语言来说,就是一个图:
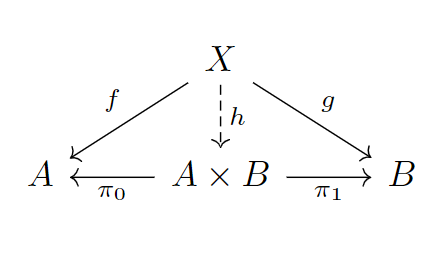
定义4.2.2: 在一个范畴中,对于对象和对象,如果与的积存在,则由两个态射唯一确定。满足对于所有对象和态射,到存在唯一的态射,使得。
大家可以尝试自己理解一下。(其中又可以记为,有)
这里有一个有趣的事实,将的所有箭头反过来就得到了!就像是0与1对偶一样,积与和也是对偶的!对偶这个概念很重要,在范畴论中,我们通常会同时研究一个范畴和其对偶范畴(也就是将所有箭头反过来)。
极限和余极限
最后来一个“王炸”,来解释一下范畴中十分十分重要的两个泛构造:极限和余极限。

这两个构造实在是涵盖了太多东西,比如和就是两种最简单的极限,和就是两种最简单的余极限。除了各种代数的概念可以用极限和余极限来表达,甚至微积分中的极限也涵盖在了这个构造之下——统一了离散和连续,代数和分析。这种令人惊掉下巴的东西,它真的存在!而它竟然又如此的简洁。(拓扑学表示很赞)
先不忙着懵逼与惊叹,其实极限和余极限就是通用的求积与求和而已——没有对象时的积就是(作为乘积的幺元),没有对象的和就是(作为求和的零元)。我们再来看看多个对象怎么求和:
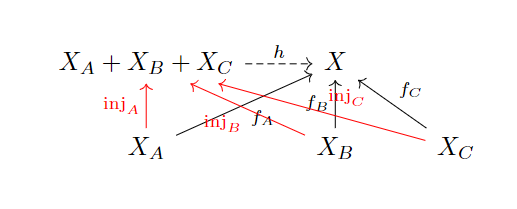
我们注意到之间可能还有态射:
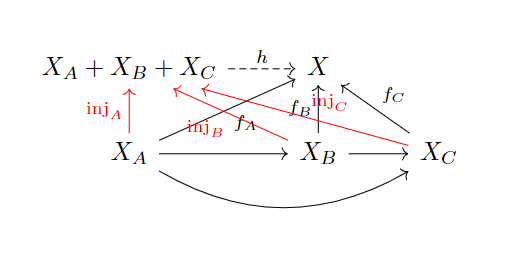
总之就要使得图里每一个这样的“锥形”(求和的语境下叫做余锥cocone),满足
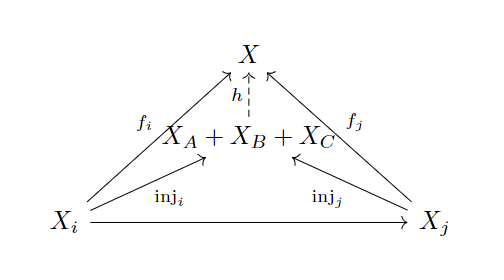
一般地,对某个范畴的求和,就叫做余极限。
要精确描述这个过程,还需要范畴论中另外一个重要的基础概念:函子(Functor)——可以把一个范畴的结构“搬”到另外一个范畴里。比如刚刚中的下标作为一个范畴,将其结构搬到范畴的中,那么这个就是一个范畴到范畴的函子:
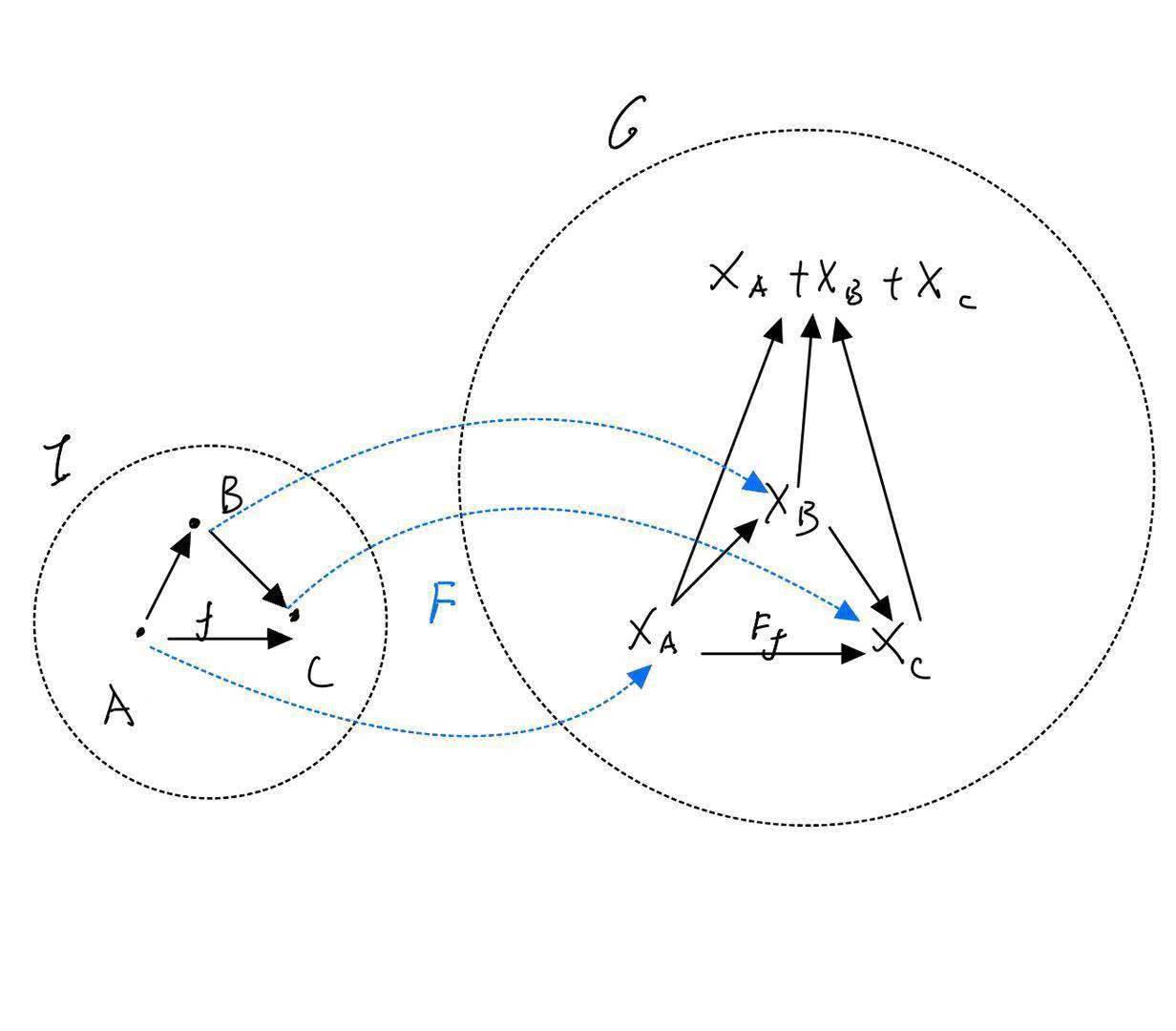
于是我们把这个记为。
定义4.3.1:对于范畴到范畴的函子,若中存在一个对象,对于中所有余锥(图4.3.6),满足,则称为函子的余极限,记为。其中余极限是唯一的。
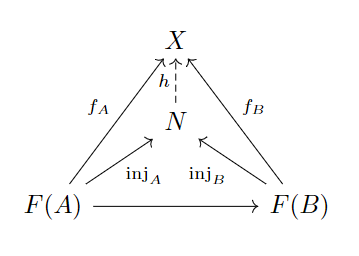
那么只有两个对象的离散的范畴,其余极限就是;对于空的范畴来说,其余极限就是。在一个范畴内,余极限未必存在(所以上面的定义中构造了一个新的范畴),但如果存在,一定是唯一的,表示满足某个性质的最优的那个对象。
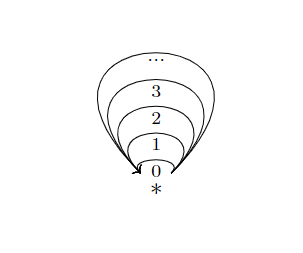
那么它是如何与分析学中的“极限”联系起来的呢?我们考虑一个实数中逼近的序列,以作为态射:
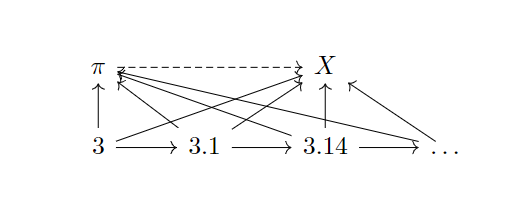
那么就是序列的余极限,表示了这个序列的最小上界。
余极限也可以表示类型中的inductive type:
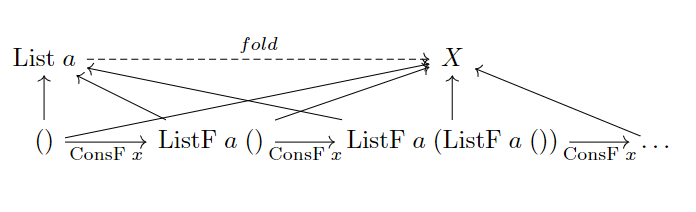
最后,余极限就是极限的对偶概念,直接将上述定义的态射反转就可以得到极限的定义:
定义4.3.1:对于范畴到范畴的函子,若中存在一个对象,对于中所有锥(图),满足,则称为函子的极限,记为。其中极限是唯一的。
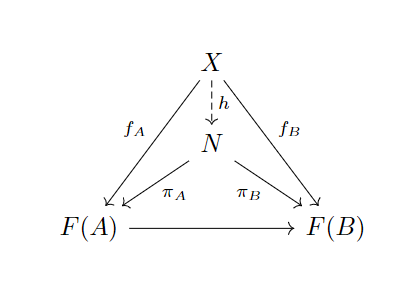
极限除了表示和之外,还可以表示coinductive type(提示,将上面List的图的箭头反转,就能得到一个Stream )。
当然范畴论中还有其它的一些泛构造,比如Kan extension,end和coend等等,这里就不一一列举了(其实是我还没看),就极限和余极限理解起来就已经够烧脑了。。
米田引理(Yoneda Lemma)
那么展现了范畴论的抽象能力 且 对其思维习惯有所理解之后,我们再进入下一个环节——范畴论的简单的应用。首先要介绍的是米田引理。这是范畴论中第一个有实质性内容的定理,它表明了一个对象与其它对象的关系(态射)决定了它本身。这也是我目前唯一能看懂一点的定理了,等我考上研我一定学,一定更新(下次丕定)。
那么在讲定理前,先引入范畴论中除了对象和态射的另两个重要的基础概念:函子和自然变换。
函子(Functor)与自然变换(Natural transformation)
函子是在范畴间保持结构的一种映射。也可以解释为范畴间的态射。有了函子,我们可以用范畴论的方法来研究范畴本身,可以抽象出范畴间的共性,可以将各种结构搬来搬去(函子式逻辑无可辩驳!),可以构造更多的范畴(比如极限和余极限)。

定义5.1.1: 函子,包含两个映射:
- 对象间的映射
- 态射间的映射
满足函子律
函子律描述的就是函子在范畴间保持结构的性质。
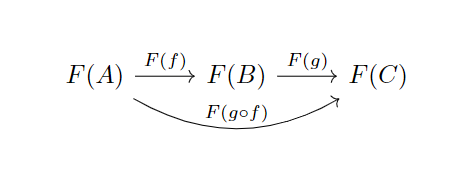
同时函子作为范畴间的态射,其复合也满足单位元与结合律,这里就不作证明了。
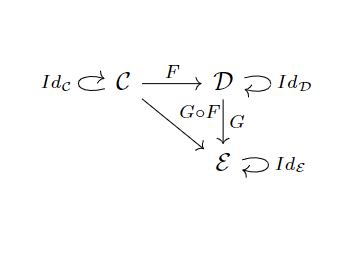
当然,既然有函子的概念,便会有其对偶的概念,叫做反变函子,这里就不作论述了。
我们最熟悉的,群作为范畴,群同态就是一个函子。同时,也正如群同态不唯一一样,两个范畴间也有各种各样的函子,甚至有很多很多都是非平凡的。于是我们需要研究不同函子之间的关系,我们又可以将函子放入范畴的框架中讨论——函子范畴,函子范畴的态射称之为自然变换。
定义5.1.2: 对于范畴以及函子,一个自然变换,
对的任意对象,可给出一个对象间的态射,称在上的分量(component),
使得对于中所有的态射,满足交换图5.1.4。
所有到上的自然变换记为。
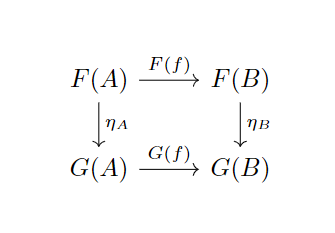
(注意,这个交换图是在范畴上的交换图,自然变换的分量就是上的态射!而下面自然变换的示意图是在范畴的范畴上,层次更高。理解这点很有帮助)
范畴的函子之间的自然变换,可以用一个示意图来直观理解:
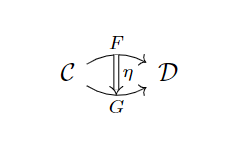
这个图揭示了范畴、函子、自然变换之间的关系。理清范畴、函子和自然变换之间的关系非常重要,这里我再补充两张图,试着帮大家理一理。有两个范畴,以及之间的函子,是到上的函子。
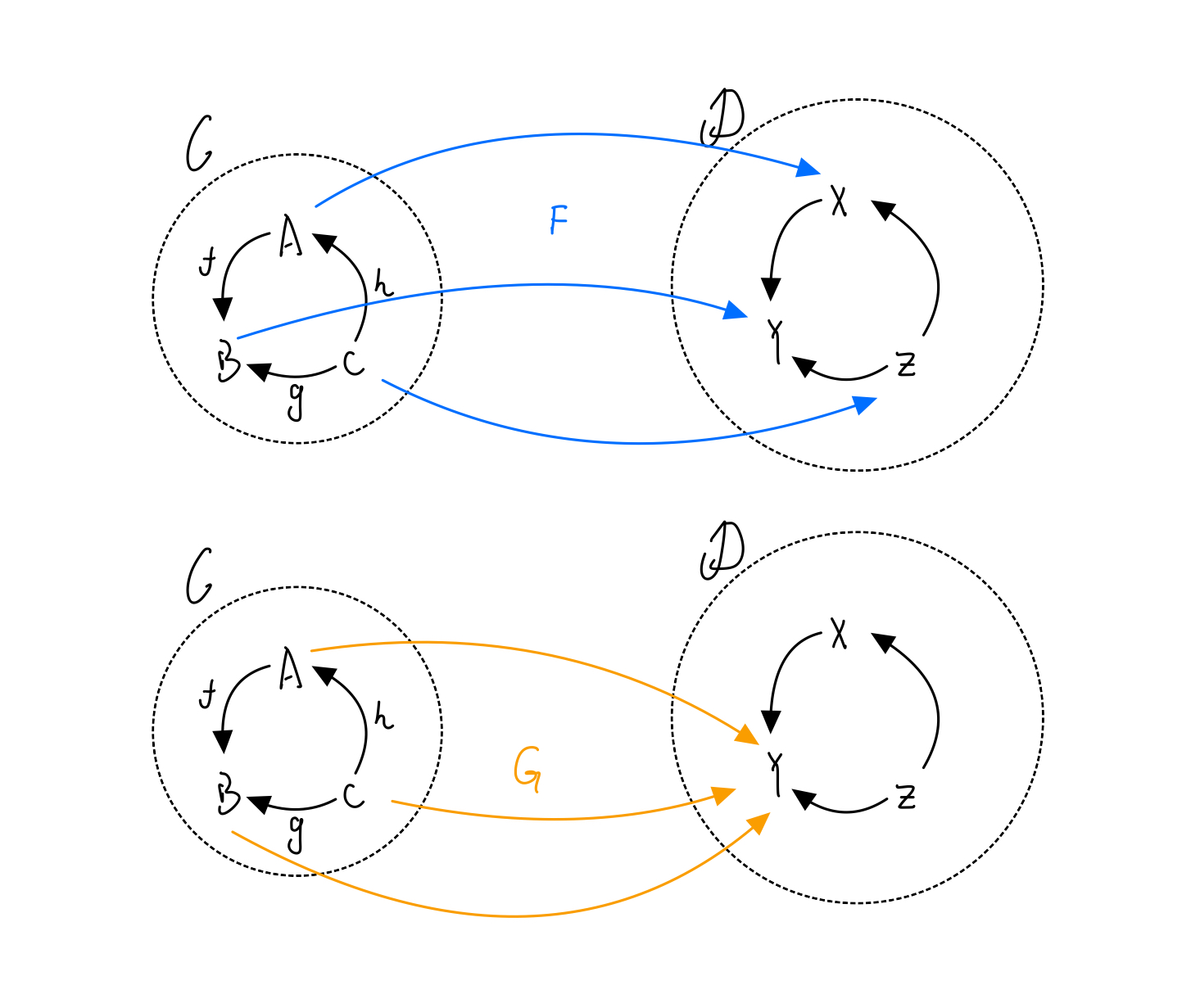
, , 分别是是在上的分量,是上的态射:
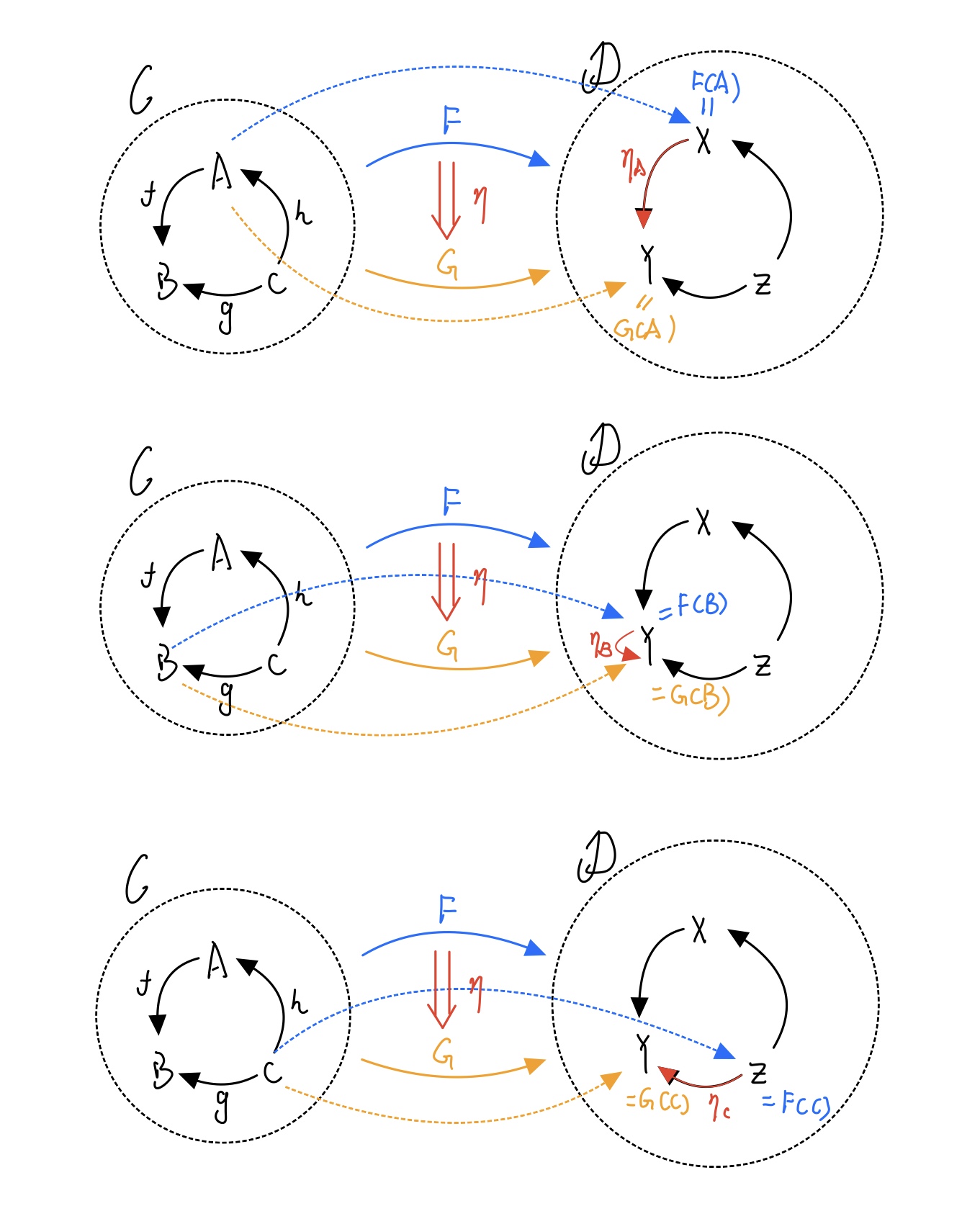
一旦觉得这三者的关系开始理不清了,就可以想起这个图来——毕竟人的脑子不好处理抽象再抽象的东西呢。
值得一提的是,自然变换有垂直和水平两个方向的复合:
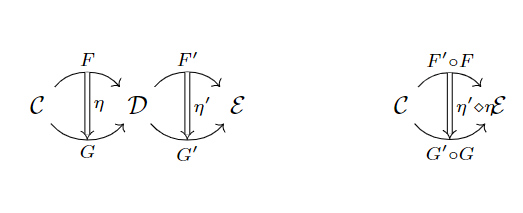
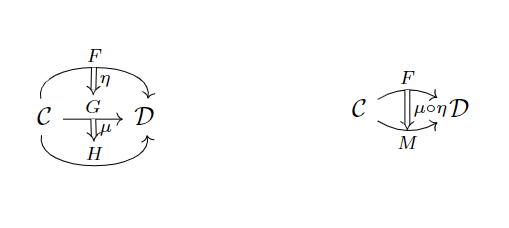
其实自然态射的水平复合的本质是函子的复合。(如果将水平复合与垂直复合结合起来看,就会得到一个等式,大家看出来了吗)
这里我们再列举几个常用的函子:
定义5.1.3: 常函子,将中的所有对象映射到中固定某个对象中,且将中的所有态射映射为的单位态射。
比如之前给出的图示里,就是一个常函子。
定义5.1.4: 单位函子,将中的所有对象和态射都映射为其自身。单位函子是一种自函子。
这两种函子都是trival的函子,我们再给出一个不那么平凡的函子:
定义5.1.5: 对于局部小范畴,以及中的一个对象,协变函子,
将中的任意对象映射为中到的所有态射组成的集合;
将中的任意态射,映射为一个函数
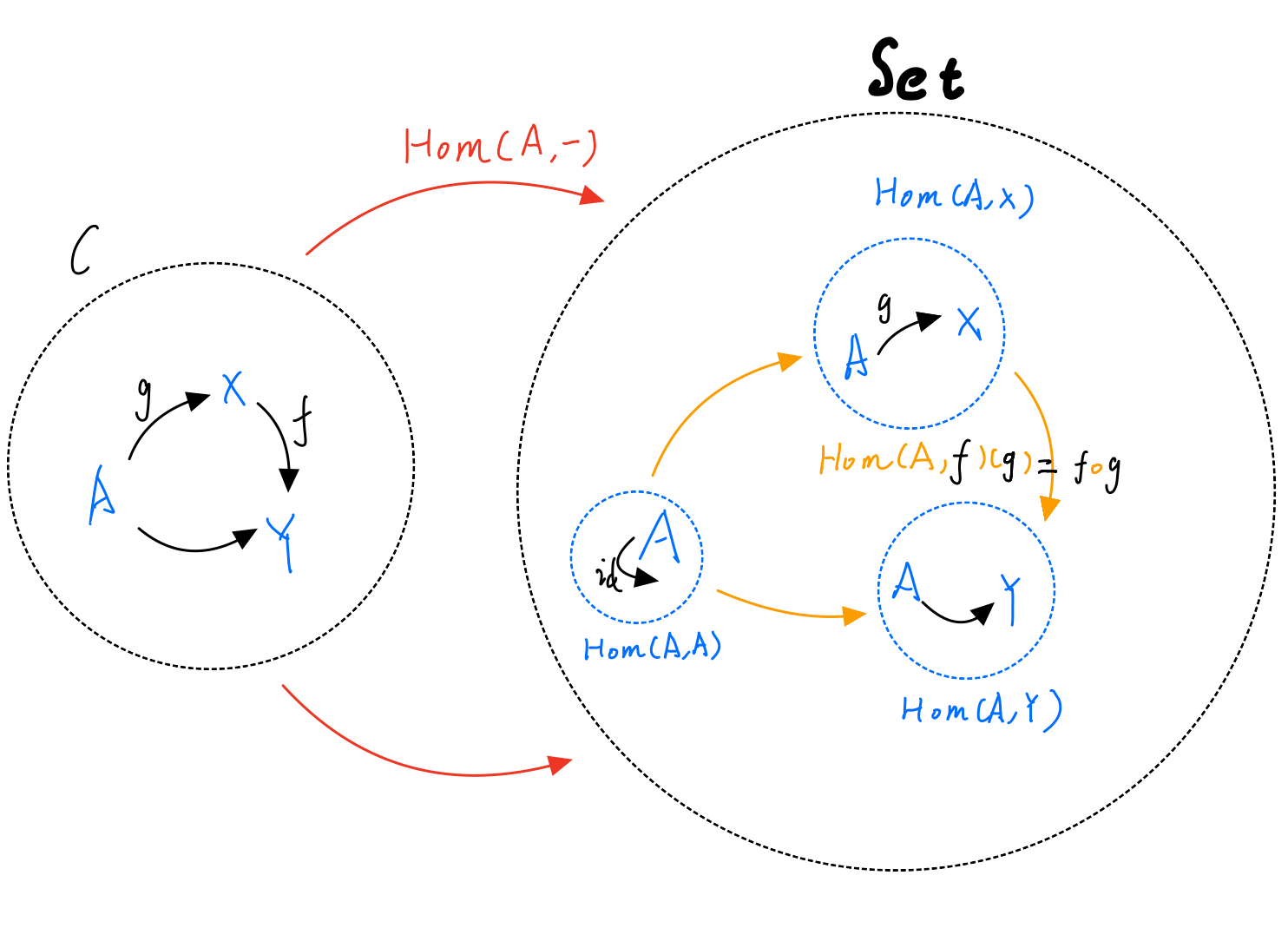
协变Hom函子是一种十分重要的一个函子,它隐含了对象的关系(态射)与对象本身相互决定的内涵,这就是下面要说的米田引理要揭示的东西了。
米田引理及其推论
经过上面一小节列了一系列定义,我们终于可以来聊一聊米田引理了。
定理5.2.1: 设局部小范畴,对于所有的函子和种的对象,
存在到的双射。即:
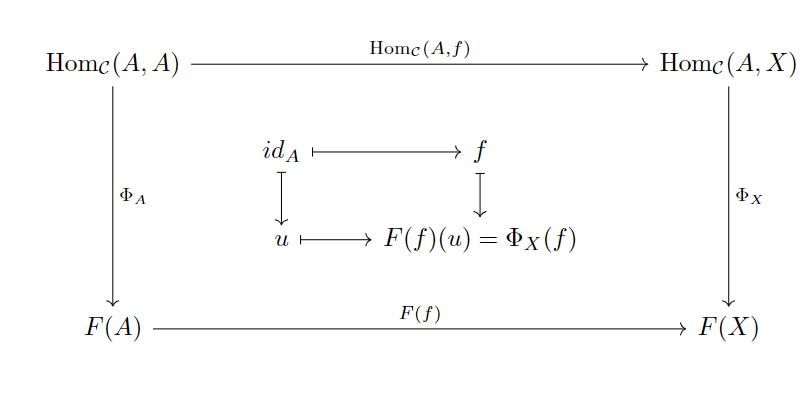
外面的交换图是到的自然变换的交换图;里面一圈是四个对象(作为集合)里面的元素,比如, ;箭头表示对应态射的具体“实现”,比如,。
解释一下这个证明的示意图:
- 到是满射:对于所有自然变换,有
- 到是满射:对于所有,自然变换由等式定义(交换图使得等式成立),其中是中的任意对象,是到的任意态射。
即与一一对应。
因为可以表示的所有关系,于是米田引理我们概括为:一个对象的所有关系决定了该对象本身。虽然这里忽略了函子的作用,但我们的确可以使用米田引理来证明这个解释:
定理5.2.2: 对象与同构,当且仅当与同构。(也就是存在isomorphism)
(提示:在米田引理,固定对象,然后取函子;然后反过来做一次,就得到了两对isomorphism)
我们也可以说,米田引理限制了范畴的”形状“,至少对象与态射之间的关系不是任意。
然后我们把目光挪回到群论中。群论中的凯莱定理,似乎也在叙述米田引理类似的事情:群元素(对象)与元素间的变换(对象间的态射)之间同构。事实上,米田引理就是凯莱定理在范畴上的推广。
定理5.2.3: 凯莱定理: 群, 则,有
为同构。
同构由米田引理取给出。需要解释的是:
函子对态射的映射,表示群对的群作用,也就是一个。
比如取,则,表示作用在群自身上,即在作用下的一个置换。
而是到的一个自然变换。
于是便表示群的一个置换群。
值得注意的是,米田引理当取范畴是函子范畴(函子为对象,自然变换是态射),也是成立的:
设函子是函子范畴的对象,对于任意函子范畴上的函子,有:
这个可以用来证明Lens两种形式的等价性。这在https://bartoszmilewski.com/2013/10/08/lenses-stores-and-yoneda/有提到。
到目前位置,我们都是用点和箭头刻画范畴的性质,仍然会感觉到十分抽象,对象是什么,态射又是什么,大脑还是接受不了这种没有实体的表示方法,虽然好像什么都说了,但好像又什么也没说一样(抽象废话)。但其实范畴是可构造的,可计算的,只是还缺乏一个自然可以表示出范畴构造的直观的语言,来帮助我们理解范畴。这时候就轮到程序语言的出场了。
计算的三位一体论(Computational Trinitarianism)
逻辑,程序(语言),范畴的三位一体——程序(语言)给出范畴的语法,范畴作为程序的语义,用程序表示逻辑(证明)。前两个说的是程序(类型)与范畴间的语法语义对偶(syntax-semantics duality),后者说的就是柯里霍华德同构。其实三者都是”计算“这一概念的三种不同的表现,当我们从其中一个方面得到的结论,那么另外两方面也会得到对应的结论。这一节,就尝试着从程序语言(类型)的角度来描述范畴论。先看看这两者是如何对应的:
| type theory | cat theory | logic |
|---|---|---|
| 类型() | 对象() | 命题() |
| 程序() | 广义对象(),态射() | 证明() |
| 调用() | 态射复合() | cut rule |
| 单位类型() | 终止对象() | true |
| 空类型() | 初始对象() | false |
| 元组() | 积() | 合取() |
| 枚举() | 和() | 析取() |
| 函数类型() | 态射() | 蕴含() |
| inductive type | colimit | 归纳法 |
这些对应是十分自然的。程序语言中的概念,能帮助我们理解范畴中的概念:
枚举的模式匹配就表达着范畴和”选择“的含义:
对应着
Left,对应着Right,对应着:either :: (a -> x) -> (b -> x) -> Either a b -> xeither f g (Left a) = f aeither f g (Right b) = g b自然满足
either f g . Left = f,either f g . Right = g在程序语言中表达函子:
xxxxxxxxxxclass Functor f wherefmap :: (a -> b) -> (f a -> f b) -- 态射的映射在程序语言中表达、证明米田引理:
xtype Nat f g = forall a. f a -> g a -- f到g的自然变换type Hom a = (a->) -- Hom函子psi :: Nat (Hom a) f -> f a -- u = \phi_A id_Apsi f = f idphi :: Functor f => f a -> Nat (Hom a) f -- \Phi_X(f) = F(f)(u)phi u = \f -> fmap f u
那么反过来也可以用范畴的概念,去理解程序语言中的概念。比如说所谓的first-class function不过就是将原(类型的)范畴嵌入到其Hom函子范畴当中,并重复这个过程。或者说将作为对象加入到原范畴中 同时将Hom函子之间的自然变换加入到原范畴中——然后得到了个笛卡尔闭范畴(cartesian closed category)。于是便可以在原范畴的基础上获得其函子范畴中那些更好的性质,以实施一些原来不可行的构造——这就是为什么first-class function有这么多优良性质的原因。
我们从一个范畴可以构造一个更高层次的范畴,来反映原范畴的某些性质,在程序语言中便是”反射“;我们又将原范畴又嵌入其中,便对应着程序语言中将某某概念的first-class化。不过在获得更好的性质的同时,通常又会带来新的约束——不至于掉入悖论的陷阱中。
而一些具体的类型系统,便对应着某些具体的范畴(摘抄自nLab),不过很惭愧的是,我自己都没学:
| type theory | cat theory |
|---|---|
| simple typed lambda calculus | cartesian closed category |
| dependent type | hyperdoctrine |
| MLTT | locally cartesian closed category |
| HoTT | elementary (∞,1)-topos |
| dependent linear type theory | indexed monoidal category |
这节只是提供看待范畴论的另外一个角度,帮助大家理解里面一些看似抽象的概念,希望大家能有豁然开朗的感觉。
所以啥是Monad
那么究竟什么是Monad呢?又如何理解 Monad不过是自函子范畴上的幺半群 这句话呢?虽然很想说,看到这还看不懂这句话,需要反省反省,但仔细想想,的确到目前为止还没有足够解释这句话的概念——这里的幺半群,和代数意义上的幺半群有些许不同,也不同于”只有一个对象的范畴“这样的范畴。
我们需要重新叙述一遍这个概念:
定义7.1: 一个在范畴上的Monad,包含一个自函子,和两个自然变换, ,满足交换图7.1与7.2。
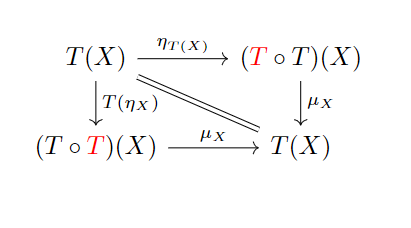
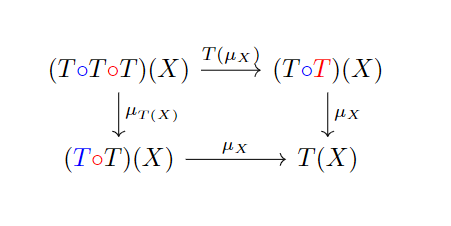
这和自函子上的幺半群又有什么关系呢?
首先是自函子范畴,其中是自函子范畴中的一些对象,自然变换和是自函子范畴中两个态射。
然后是类似幺半群的性质。为了更好地体现幺半群的本质,我们暂且将functor的复合符号,换成符号笛卡尔积,那么:
- 对应幺半群的二元运算,比如对应右结合,对应左结合。左右结合相等,就是交换图7.2所要描述的law。
- 对应幺半群的单位元,比如对应左乘一个幺元,对应右乘一个幺元。左乘幺元等于右乘幺元 且不变,就是交换图7.1所要描述的law。
我们说定义一个幺半群,而形式相同,我们也说Monad也定义了一个幺半群。因为Monad定义在一个自函子范畴上,所以我们便可以说,Monad不过是自函子范畴上的幺半群。
形式上终于搞明白了吧~
在程序语言中,Monad通常表示带effect的计算。比如,可以表示一个的计算结果,带有一个effect序列。一般要求effect具有传递性(对应结合律),可以通过组合使其变成一个effect;同时还要求一个单位的effect,用于升格一个不带作用的计算(对应单位元)。而Monad的抽象,天然满足这两个朴素的假设,用表示effect的组合(Haskell中就是join),表示单位的effect(Haskell中就是return)。这就是我们用Monad表示effect的原因。
而或者说join在日常编程中不怎么符合人体工程学,在实践上,我们通常会使用其等价的形式。(>>=)或者(<=<)::Monad t => (b -> t c) -> (a -> t b) -> (a -> t c)。后者作为态射的组合,与一些对象组成一个Keisli范畴,这个(g<=<f)便定义为。大家可以自行验证其结合律和单位元律(作为单位元)。
那么Monad在程序中的意义的也大概讲清楚了吧?
总结
这篇文章到这里也就差不多结束了。总结本文的一个结构:
- 为了用代数的目光看待范畴,从群引入范畴的定义;
- 再用范畴表示一些熟悉的数学对象,以体现范畴的通用性;
- 然后通过一些基本的例子展示了范畴论基本思想,并介绍了一些范畴论的基本语言;
- 使用范畴论解决一些问题(米田引理)
- 从程序语言的角度来重新看待范畴论,以提供一个更具体的视角来理解范畴论
- 最后回归到一个日经问题——Monad是什么
希望大家可以通过我这篇文章,能了解到一些范畴论的一些知识,至少不再恐惧那些看起来不知所云的范畴论抽象,或者作为今后学习范畴论的敲门砖,我和大家共同学习,共同进步(我其实也只是入门)。
参考
- https://ncatlab.org/nlab/show/relation+between+type+theory+and+category+theory "relation between type theory and category theory"
- https://ncatlab.org/nlab/show/computational+trinitarianism "computational trinitarianism"
- https://en.jinzhao.wiki/wiki/Monad_(category_theory) "Monad"
- https://en.jinzhao.wiki/wiki/Limit_(category_theory) "Limit"
- https://zhuanlan.zhihu.com/p/91153185 "1+1=2"
- 如何理解Yoneda lemma(米田引理)的重要性? - 知乎 https://www.zhihu.com/question/360451548/answer/1522274000
