猫和老鼠（范畴和代数）

本文简单列举下范畴和其它抽象代数的关系。（不正式地）

范畴作为代数系统

域去掉乘法交换律、逆元、单位元（将乘法群弱化成半群）得到环
取环的加法并去掉交换律（阿贝尔群弱化成群）得到群
群去掉逆元得到幺半群
幺半群弱化封闭性得到范畴（元素的运算是在一个Domain的运算，而态射的复合是在多个Domain上的运算）
格去掉上下界得到序
序范畴 $\le$ 的方式）

remark: 半群（->半范畴），一般作为辅助性的结构看待。
remark: 范畴是一个十分松散的代数结构，与之相对的群是一个十分紧凑的代数结构。群作为一个只有一个对象且态射都是同构的范畴，溶解掉过强的”联系“（去掉可逆）就得到了幺半群，再将”一个对象“拆散就得到了一般的范畴。

群，格和范畴中概念的一些对应关系

在上面代数结构的依赖中，有几个关键的结点：群，格，范畴。（当然其它的也十分十分的重要）这三者关系其实联系十分密切，下表来展示其中一些对应关系：

群	范畴	格
-	对象	元素
元素	态射	偏序关系
二元运算	复合	传递性
单位元	单位态射	自反性
逆运算	同构态射	对称性
$f: G \simeq G'$ )	$F: \mathcal{C} \rightarrow \mathcal{D}$ )	$f: L \simeq L'$ )
$x \mapsto a\cdot x$ )	$\mathrm{Hom}_\mathcal{C}(A, -)$ )	$a\le -$ )
$\mathrm{sym}\, G$ )	$\mathbf{Set}^\mathcal{C}$ )	上闭集合格
凯莱定理	米田引理
子群	子范畴	子格
商群	商范畴	商格
-	$\times$ )	$\wedge$ )
-	$+$ )	$\vee$ )
-	$\lim\limits_{\leftarrow} F$ )	$\bigwedge\limits_{L' \subset L}L'$ )
-	$\lim\limits_{\rightarrow} F$ )	$\bigvee\limits_{L' \subset L}L'$ )

remark: 函子范畴中对象是函子，态射是自然变换。米田嵌入和米田引理就是说明如何用函子范畴表示一般的范畴。就如同对称群之于一般群一样。
remark: $F:\mathcal{I} \to \mathcal{C}$ $\mathcal{C}$ 选择 $F$ $\mathcal{C}$ 的一个图示(diagram)。
remark: （余）极限就表示满足一个图示（表示某个性质）的最好的那个对象。（比如取态射为偏序关系就是子集的最大下界）。

用范畴的语言描述代数

上面展示的是范畴作为代数系统，与其它代数结构之间的关系。而我们还会用范畴的内部的语言反过来描述各种代数系统。

第一种方式：将各种代数作为范畴的对象态射 $\mathbf{Grp}, \mathbf{Vect}_\mathrm{k}, \mathbf{Ring}, \mathbf{R}\!-\!\mathrm{Mod}, \mathbf{Cat}\cdots$ 等等范畴了。

在这种方式下，各种代数系统的基本同态定理就可以用一个交换图来表达了：

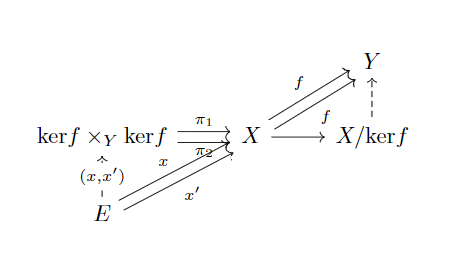
$f: X\to Y$ $\mathrm{ker}f \times_Y \mathrm{ker}f = \{(x,x')|f(x) =f(x')\}$ $f$ 导出的等价关系。那么该交换图就是说：

$X/\mathrm{ker}f = \{[x]_{\mathrm{ker}f}| x \in X\}$ $\mathrm{ker}f \times_Y \mathrm{ker}f$ $X$ 的coequalizer（一个余极限）。
$\mathrm{ker}f \times_Y \mathrm{ker}f$ $X$ $Y$ 的一个equalizer（一个极限），称为kernel pair。

第二种方式：在范畴中添加新的结构（用函子来表达），来表示代数结构。比如用幺半范畴表示幺半群。

定义1 $\mathcal{C}$ 装备有
$\otimes: \mathcal{C} \times \mathcal{C} \to \mathcal{C}$
$1$ $\otimes$ 的单位元
$\alpha: (-\otimes -)\otimes - \to -\otimes (-\otimes -)$
$\alpha_{x,y,z}: (x\otimes y)\otimes z \to x\otimes (y\otimes z)$ ，
称为结合子(associator)
$\lambda: 1 \otimes - \to -$
$\lambda_x: 1 \otimes x \to x$
称为左单位子(left unitor)
$\rho: - \otimes 1 \to -$
$\rho_x: x \otimes 1 \to x$
称为右单位子(right unitor)
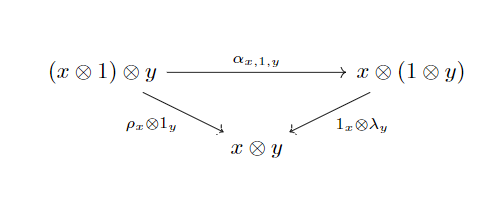
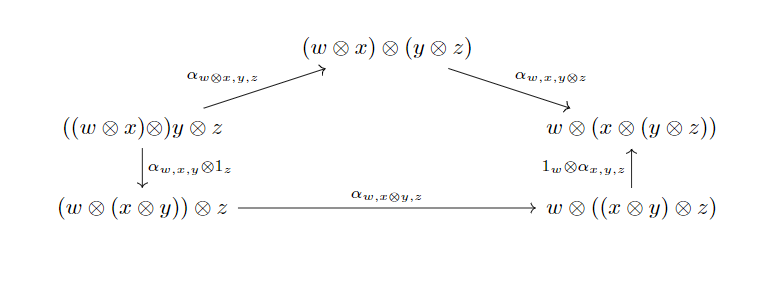
满足以下两个交换图

那么就可以在幺半范畴上定义一个幺半群

定义2 $(\mathcal{C}, \otimes,1)$ $M$ 装备有
$\mu: M \otimes M \to M$
作为乘法
$\eta: 1 \to M$
作为单位元
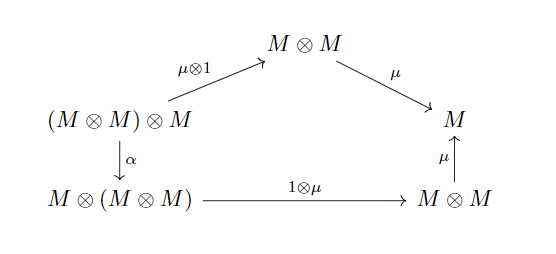
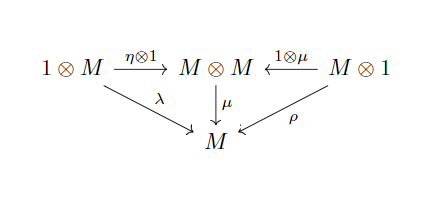
满足交换图：

$\mathcal{C}$ $\otimes$ $1$ 为单位函子。

范畴和分析？

除了用范畴的语言来描述代数的性质，我们也可以用范畴的语言来描述分析学的一些定理。

比如说套闭区间原理说的是：任意套闭区间序列存在一个极限。

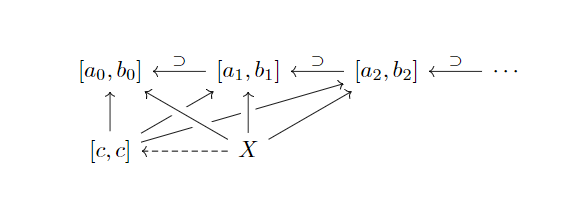
interal

当然，范畴也可以描述一个拓扑。任意图表存在的余极限（任意并为开集），有限图表存在极限（有限交为开集）的范畴可以作为一个拓扑来看待。